¿Que es la probabilidad?
La probabilidad es la mayor o menor posibilidad de que ocurra un hecho.
Mide de forma cuantitativa la seguridad o no de que pueda suceder un evento.
Ej: la probabilidad de sobrevivir a una operación es del 50%.
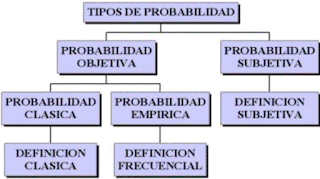
Hay dos tipos de probabilidad:
- Probabilidad objetiva: es la que se calcula conociendo el total de los resultados posibles.
- Probabilidad subjetiva: grado de confirmación de un determinado suceso a partir de la evidencia posible.
Probabilidad subjetiva o personalística
La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada.
Ej: los epidemiológicos se basan en la experiencia para afirmar que el próximo invierno la epidemia de gripe tendrá una probabilidad del 0,0018 (180 casos por 100.000 habitantes).
Probabilidad clásica o "a priori"
Las probabilidades se calculan con un razonamiento abstracto.
Si un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos poseen unas caracteristicas E, la probabilidad de ocurrencia de E es igual a m/N.
Probabilidad relativa o "a posteriori"
Si un suceso es repetido
un GRAN número
de veces, y
si algún evento resultante, con la característica
E, ocurre
m
veces,
la
frecuencia
relativa
de la ocurrencia
E, m/n, es aproximadamente
igual a la
probabilidad de ocurrencia de E.
Ley de los grandes números
Cuando
no sea posible calcular la probabilidad mediante la regla de Laplace
necesitaremos hacerlo mediante las frecuencias relativas. Nos estaríamos
basando en los que se conoces como la ley de los grandes números.
La
ley de los grandes números es un teorema fundamental de la teoría de la
probabilidad que indica que si repetimos muchas veces (tendiendo al infinito)
un mismo experimento, la frecuencia de que suceda un cierto evento tiende a ser
una constante.
Sucesos
Hay 2 tipos de sucesos:
- Sucesos compatibles: dados dos sucesos o más (por ej. A y B), diremos que son incompatibles o mutuamente excluyentes cuando su realización simultánea es imposible y tienen algún suceso elemental común.
- Sucesos incompatibles: dados dos sucesos o más (por ej. A y B), diremos que son incompatibles o mutuamente excluyentes cuando su realización simultánea es imposible , no teniendo ningún suceso elemental común Ej. de sucesos incompatibles: lanzar un dado y que salga par e impar a la vez, ser a la vez hombre y mujer; O el suceso A y su suceso contrario Ac A y B no tienen elementos comunes: son conjuntos disjuntos, forman una partición muestral y la suma de ellos el espacio muestral.
Teoría de la probabilidad
Teorema de Bayes
El
teorema de Bayes
es utilizado para calcular la probabilidad de un suceso, teniendo información
de antemano sobre ese suceso. Desarrollado por el reverendo Thomas Bayes
en el siglo XVII, el teorema de Bayes
es una extensión de lo que ha aprendido hasta ahora acerca de la probabilidad
condicional.
Distribución binomial
Para construir una distribución binomial es necesario conocer el número de pruebas que se repiten y la probabilidad de que suceda un éxito en cada una de ellas.
La fórmula es la siguiente:
Distribución de Poisson
- Se usa en situaciones donde los sucesos son impredecibles de ocurrencia aleatoria. No se sabe el total de posibles resultados.
- Permite determinar la probabilidad de ocurrencia de un suceso con resultado discreto.
- Es útil cuando la muestra o segmento n es grande y la probabilidad de éxitos p es pequeña.
- Se utiliza cuando la probabilidad del evento que nos interesa se distribuye dentro de un segmento n, dado como por ejemplo distancia, área, volumen o tiempo definido




Comentarios
Publicar un comentario